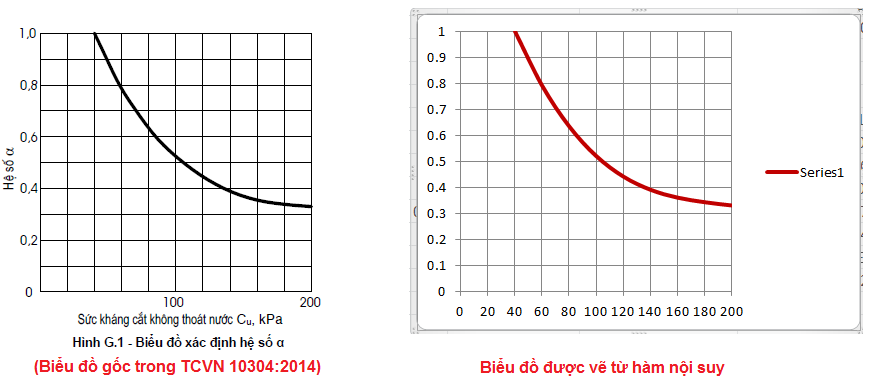
Ngày nay, không mấy ai tra bảng một cách thủ công để phục vụ cho các tính toán, nhưng nghịch lý ở chỗ các tiêu chuẩn vẫn chỉ thể hiện các bảng tra mà hầu như không đưa ra các công thức để tạo ra các bảng đó. Một cách mà các kỹ sư có thể làm là sử dụng đa thức nội suy Newton để tạo hàm nội suy cho bảng tra.
Tóm tắt phương pháp
Nếu biết trước n điểm (X1,Y1); (X2,Y2); ...; (Xn,Yn), đa thức nội suy có thể viết thành
y = A1 + A2*(x-X1) + A3*(x-X1)*(x-X2) + ... + An*(x-X1)*(x-X2)*...*(x-Xn-1)
Việc tiếp theo là phải tìm ra A1, A2, .., An
Để tìm A1, thay x = X1 và y = Y1 vào biểu thức, ta tìm được A1 = Y1
Để tìm A2, thay x = X2 và y = Y2 vào biểu thức, ta tìm được A2 = (Y2-A1)/(X2-X1) với A1 đã tìm được phía trên
Lần lượt cho đến khi thay x = Xn-1 và y = Yn-1 ta sẽ tìm được An-1
Cuối cùng khi thay x = Xn, y = Yn ta sẽ tìm ra được An
Sau khi tìm được đầy đủ các hệ số, ta có thể phân tích đa thức để đưa về dạng y = C1 + C2*X + C3*X2 + ... + *Xn-1
Áp dụng
Việc chọn đa thức nội suy phụ thuộc vào dạng biểu đồ, thông thường chi cần dùng một hàm bậc 3 là đã đủ để miêu tả một đường cong đơn giản, nghĩa là chỉ cần chọn ra 4 điểm để thay vào đa thức nội suy.
Ví dụ đối với biểu đồ trong hình G1 của TCVN 10304:2014, như hình phía dưới, ta chỉ cần chọn ra 4 điểm, trong đó có 2 đầu mút của biểu đồ và 2 vị trí ở khoảng giữa
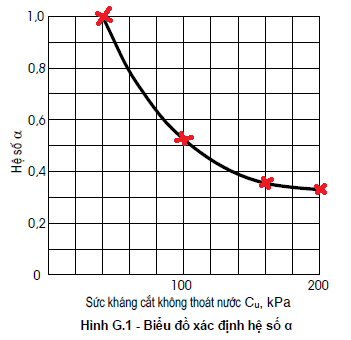
Tôi chọn trên đồ thị 4 điểm có giá trị lần lượt là (các điểm này được tra bằng thủ công, dóng trên biểu đồ, ước lượng một giá trị gần đúng)
- X1 = 40; Y1 = 1
- X2 = 100; Y2 = 0.52
- X3 = 160; Y2 = 0.36
- X2 = 200; Y2 = 0.33
Đa thức nội suy có thể viết thành
y = A1 + A2*(x-40) + A3*(x-40)*(x-100) + A4*(x-40)*(x-100)*(x-160)
Khi thay x = 40 và y = 1; ta thu được A1 = 1
Tiếp tục thay x = 100 và y = 0.52, ta thu được A2 = -0.008
Tiếp tục thay x = 160 và y = 0.36, ta thu được A3 = 0.000038125
Cuối cùng thay x = 200 và y = 0.33, ta thu được A4 = -0.0000001579861
Thay A1, A2, A2, A4 vào đa thức trên và triển khai, ta thu được hàm nội suy bậc 3 có dạng: y = C1 + C2*x + C3*X2 + C4*X3, trong đó:
- C1 = 1.598888888888890
- C2 = -0.018393055555556
- C3 = 0.000091840277778
- C4 = -0.000000157986111
Từ hàm nội suy thu được, ta có thể tái tạo lại đồ thị và so sánh như hình phía dưới, kết quả như chúng ta có thể thấy:
Quan tâm Zalo KetcauSoft để theo dõi các bài viết và tài liệu mới
